本文参考《Google机器学习速成课程》分类
评估方式
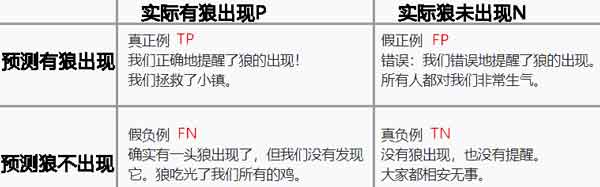
准确率|识别率 Accuracy=\dfrac{TN+TP}{All}
错误率|误分类率 Error Rate=\dfrac{FP+FN}{All}
当使用分类不平衡的数据集时,准确率并不能反映全面情况
精确率|精度 Precision=\dfrac{TP}{TP+FP}
真正例率|敏感度|召回率 Recall=\dfrac{TP}{P}
真负例率|特效性 Specificity=\dfrac{TN}{N}
精确率和召回率往往此消彼长
分类操作工程化
# 线性多分类器
linear_classifier = tf.estimator.LinearClassifier(
feature_columns=construct_feature_columns(training_examples),
optimizer=my_optimizer
)
# 获取实值预测概率
training_probabilities = linear_classifier.predict(input_fn=predict_training_input_fn)
training_probabilities = np.array([item['probabilities'] for item in training_probabilities])
#获得一个多维数组[[0.813 0.184][0.821 0.179]...[0.557 0.443]]
# 使用Sklearn 的 log_loss 函数可基于这些概率计算对数损失函数
training_log_loss = metrics.log_loss(training_targets, training_probabilities)
#LinearClassifier.evaluate 可计算准确率和 AUC 等实用指标
predict_validation_input_fn = lambda: my_input_fn(validation_examples,
validation_targets["median_house_value_is_high"],
num_epochs=1,
shuffle=False)
evaluation_metrics = linear_classifier.evaluate(input_fn=predict_validation_input_fn)
print "AUC on the validation set: %0.2f" % evaluation_metrics['auc']
print "Accuracy on the validation set: %0.2f" % evaluation_metrics['accuracy']
ROC曲线
在逻辑回归里,我们会设一个阈值,大于这个值的为正类,小于这个值为负类。如果我们减小这个阀值,那么更多的样本会被识别为正类。这会提高正类的识别率,但同时也会使得更多的负类被错误识别为正类。为了形象化这一变化,引入ROC(Receiver Operating Characteristic)
ROC曲线有个很好的特性,当测试集中的正负样本的分布变化的时候(类不平衡现象),ROC曲线能够保持不变,因此更适合用于评价一个分类器好坏
AUC(Area Under Curve)被定义为ROC曲线下的面积,AUC值越大的分类器,正确率越高
# 绘制 ROC 曲线
# 使用类别概率(例如由 LinearClassifier.predict 和
validation_probabilities = linear_classifier.predict(input_fn=predict_validation_input_fn)
#只要预测为正的那一列
validation_probabilities = np.array([item['probabilities'][3] for item in validation_probabilities])
#使用Sklearn的 roc_curve 来获得所需的TP和FP
false_positive_rate, true_positive_rate, thresholds = metrics.roc_curve(
validation_targets, validation_probabilities)
#FP:[0.0000e+00 0.0000e+00 2.6788e-04 ... 9.9785e-01 9.9785e-01 1.0000e+00]
#TP:[7.8926e-04 2.3677e-03 2.3677e-03 ... 9.9921e-01 1.0000e+00 1.0000e+00]
#th:[9.9380e-01 9.7655e-01 9.7536e-01 ... 1.3434e-05 8.5868e-06 6.9566e-14]
plt.plot(false_positive_rate, true_positive_rate, label="our model")
plt.plot([0, 1], [0, 1], label="random classifier")
_ = plt.legend(loc=2)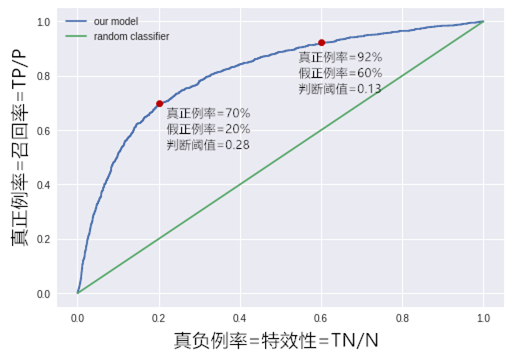
![[TF.6]正则化Regularization](https://blog.mclover.cn/wp-content/themes/slanted/img/thumb-medium.png)